競馬の着順をモデリングしてみた

2024年度社心院生リーグのLTネタ．放置してましたがここらで供養しておきます．
競馬
統計モデリング
Stan
Author

Hidezo Suganuma

Published

October 15, 2025

はじめに

競馬はたいへん楽しい娯楽だが，同時に非常に難しいゲームでもある．レースの結果じたいが不確実だし，特にパリミュチュエル市場ではオッズが他者の投票に依存するという意味で社会的な不確実性も伴う．安定的にプラスのリターンを得られるよう適応的に意思決定することは容易でない．

学部生時代にバイト代を注ぎ込んだ結果そのセンスがないことを自覚した自分にとって，競馬で勝つために残されたほぼ唯一の道筋が機械学習や統計的手法の活用である．そもそも人間の認知的能力にも限りがあるわけだから，直感や思考に頼っていたプロセスをそれらに置き換えることは合理的かつ真摯な態度であるといえなくもないはずだ．

自分はCS系の専攻でもない一介の貧乏大学院生にすぎないので，自前で大規模なデータベースを用意したり巨大なモデルを学習させたりするのはなかなかに骨が折れるところである（これまで馬券で失った金で可能だったのではないか？）．そこでもう少し手軽な代替案として（？）階層ベイズモデルにより競馬の着順をモデリングしてみよう，というのがこの記事の趣旨である．

なお，根本となるアイデアはこちらのブログ記事を参考にしている．

データ

JRA-VAN Data Lab.から取得した，2021年生産馬の世代限定戦を使用する．最初の新馬戦からダービーまでの中央競馬全レースが対象で，レース数は1389，出走頭数は4661頭だった．

馬ごとの出走回数の分布は以下のとおり．

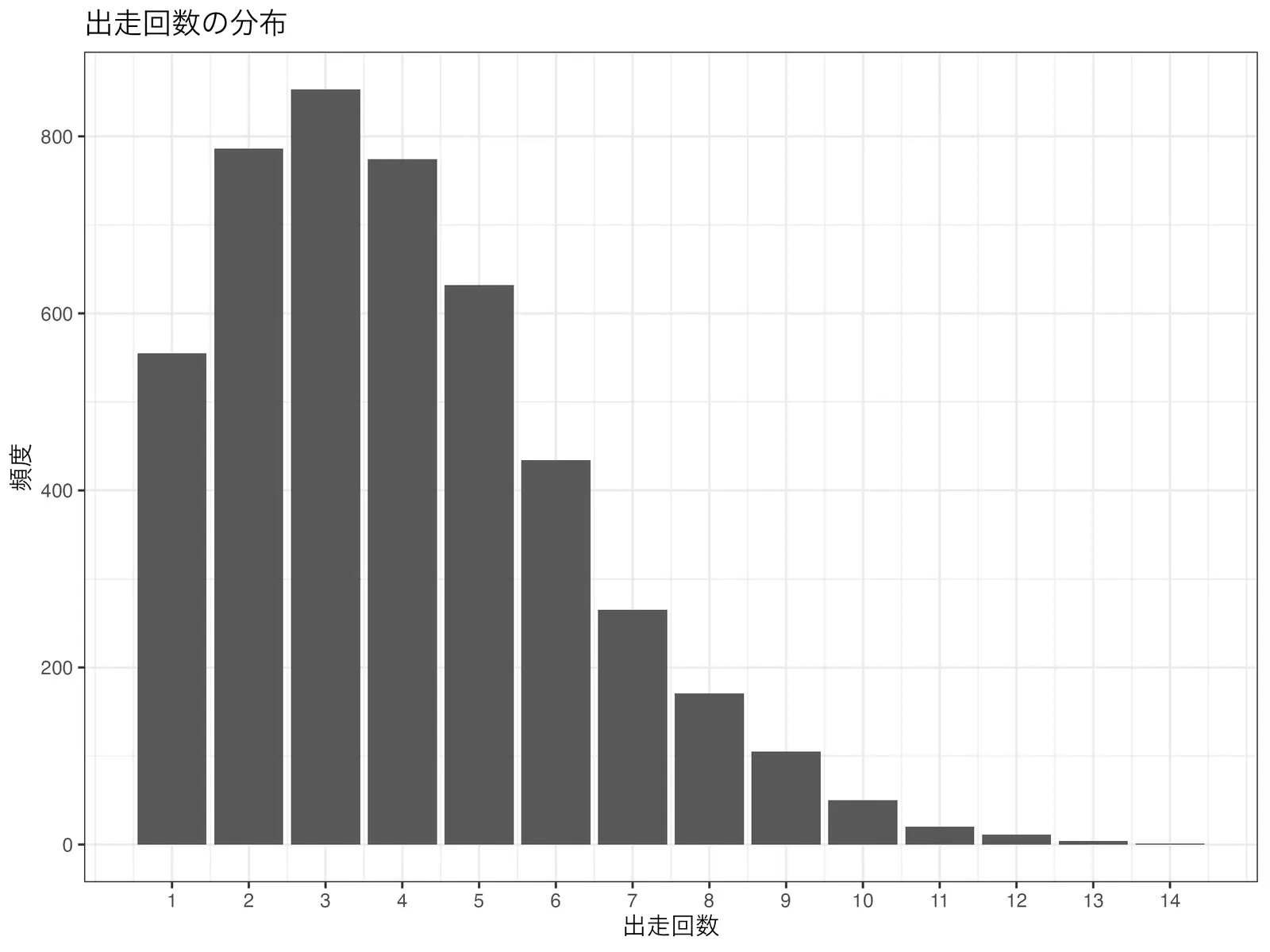
また，各レースの出走頭数の分布は以下のようになった．

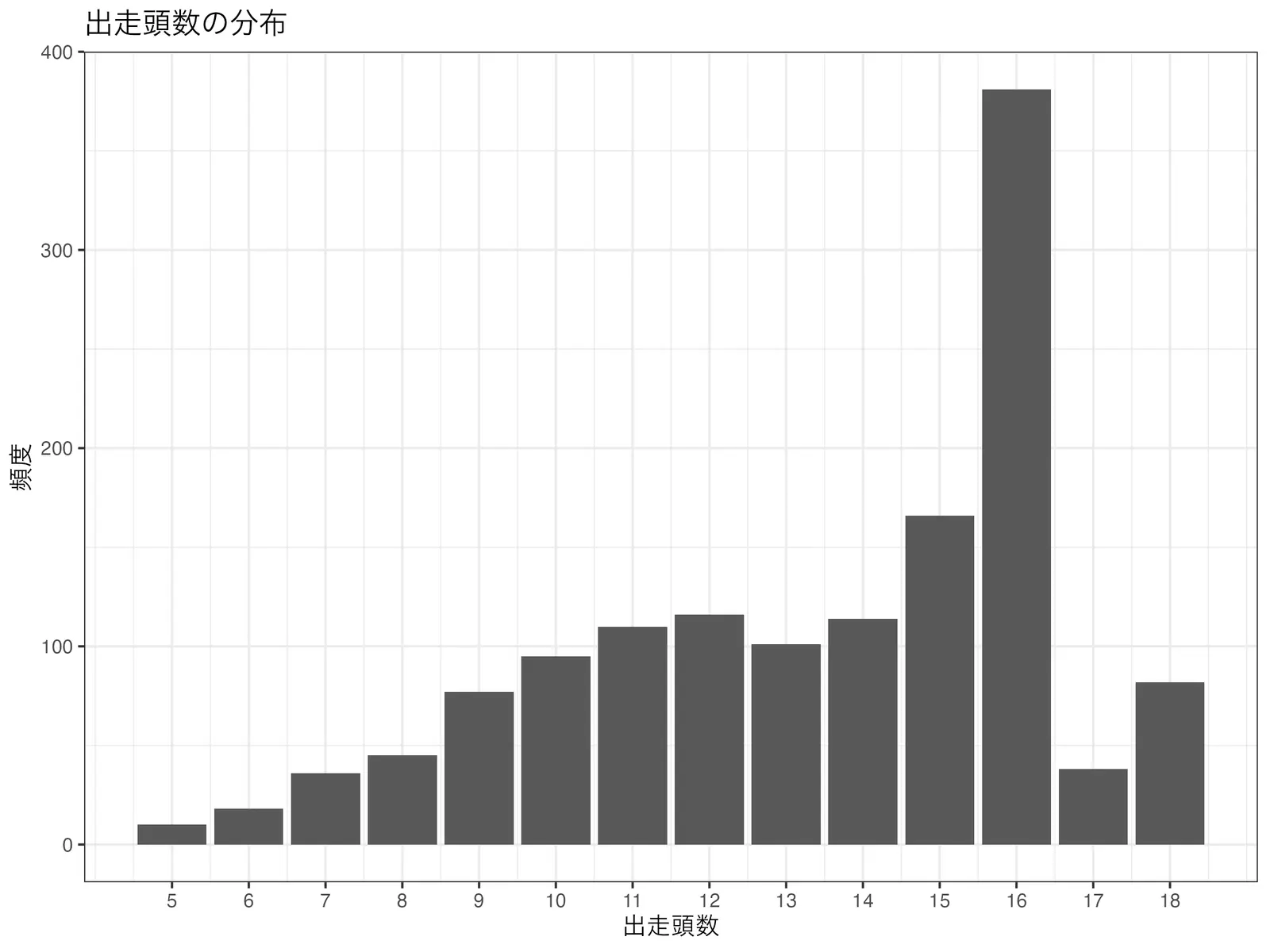
フィッティングの際は，ダービーを除く全レースのデータを使用する（詳細は後述）．

モデル

あるレース\(r\)において，馬\(h\)が発揮するパフォーマンス\(f\)が正規分布

\[ f_{r,h} \sim \mathcal{N}(\mu_{h} + \mu_{j}, \sigma_{h}^2 + \sigma_{j}^2) \]

に従うとする．\(\mu_{h}\)は馬\(h\)がもつ平均的な競争能力，および\(mu_{j}\)は騎手\(j\)の平均的な巧みさを表すパラメータであり，\(\sigma_{h}\)および\(\sigma_{j}\)はその不確実性を表している．

レースで観測される「着順」は，出走馬のパフォーマンス\(f_{r,h}\)の順序に基づいて決まるものとする（\(h\in{1,2,3,\dots,N(r)}\)）．言い換えると，レース\(r\)で馬\(h\)が\(k\)着になるのは，パフォーマンス\(f_{r,h}\)が\(N(r)\)頭の出走馬のなかで\(k\)番目である場合である．要するに，「馬の強さ」と「騎手のうまさ」を足し合わせた結果が小さいほど良い着順になるというシンプルなモデルである．

\(\mu_{h}\)および\(\mu_{j}\)はそれぞれ平均0の正規分布に従うと仮定し，以下のような事前分布をおく．

\[ \begin{aligned} \mu_{h} &\sim \mathcal{N}(0, \sigma_{\mu_h}^2) \\ \mu_{j} &\sim \mathcal{N}(0, \sigma_{\mu_j}^2) \\ \sigma_{\mu_h} &\sim \mathrm{Exponential}(\lambda=5) \\ \sigma_{\mu_j} &\sim \mathrm{Exponential}(\lambda=5) \\ \end{aligned} \]

Stanによる実装

model.stan
data {
  array[14] int N_race;
  int N_horse;
  int N_jockey;
  array[sum(N_race), 18] int HorseID;
  array[sum(N_race), 18] int JockeyID;
}

transformed data {
  // Index for querying results
  array[14] int Start;
  for (i in 1:14) {
    if (i == 1) {
      Start[i] = 0;
    } else {
      Start[i] = sum(N_race[1:(i-1)]);
    }
  }
}

parameters {
  // Results
  array[N_race[1]] ordered[5] performance5;
  array[N_race[2]] ordered[6] performance6;
  array[N_race[3]] ordered[7] performance7;
  array[N_race[4]] ordered[8] performance8;
  array[N_race[5]] ordered[9] performance9;
  array[N_race[6]] ordered[10] performance10;
  array[N_race[7]] ordered[11] performance11;
  array[N_race[8]] ordered[12] performance12;
  array[N_race[9]] ordered[13] performance13;
  array[N_race[10]] ordered[14] performance14;
  array[N_race[11]] ordered[15] performance15;
  array[N_race[12]] ordered[16] performance16;
  array[N_race[13]] ordered[17] performance17;
  array[N_race[14]] ordered[18] performance18;
  
  // Parameters
  // Horse
  vector[N_horse] mu_pf_h;
  vector<lower=0>[N_horse] sigma_pf_h;
  
  // Jockey
  vector[N_jockey] mu_pf_j;
  vector<lower=0>[N_jockey] sigma_pf_j;

  // Hyperparameters
  real<lower=0> sigma_mu_h;
  real<lower=0> sigma_mu_j;

}

model {
  // Prior
  target += normal_lpdf(mu_pf_h | 0, sigma_mu_h);
  target += normal_lpdf(mu_pf_j | 0, sigma_mu_j);
  target += exponential_lpdf(sigma_mu_h | 5);
  target += exponential_lpdf(sigma_pf_h | 5);
  target += exponential_lpdf(sigma_mu_j | 5);
  target += exponential_lpdf(sigma_pf_j | 5);

  // Likelihood
  for (d in 5:18) {    
    array[N_race[d-4], d] int horse;
    array[N_race[d-4], d] int jockey;
    
    for (i in 1:N_race[d-4]) {
      for (r in 1:d) {
        horse[i, r] = HorseID[Start[d-4]+i, r];
        jockey[i, r] = JockeyID[Start[d-4]+i, r];
      }
    }

    for (i in 1:N_race[d-4]) {
      for (r in 1:d){
        real mu = mu_pf_h[horse[i, r]] + mu_pf_j[jockey[i, r]];
        real sigma = sqrt(
          square(sigma_pf_h[horse[i, r]]) + square(sigma_pf_j[jockey[i, r]])
        );
        if (d == 5) target += normal_lpdf(performance5[i, r] | mu, sigma);
        if (d == 6) target += normal_lpdf(performance6[i, r] | mu, sigma);
        if (d == 7) target += normal_lpdf(performance7[i, r] | mu, sigma);
        if (d == 8) target += normal_lpdf(performance8[i, r] | mu, sigma);
        if (d == 9) target += normal_lpdf(performance9[i, r] | mu, sigma);
        if (d == 10) target += normal_lpdf(performance10[i, r] | mu, sigma);
        if (d == 11) target += normal_lpdf(performance11[i, r] | mu, sigma);
        if (d == 12) target += normal_lpdf(performance12[i, r] | mu, sigma);
        if (d == 13) target += normal_lpdf(performance13[i, r] | mu, sigma);
        if (d == 14) target += normal_lpdf(performance14[i, r] | mu, sigma);
        if (d == 15) target += normal_lpdf(performance15[i, r] | mu, sigma);
        if (d == 16) target += normal_lpdf(performance16[i, r] | mu, sigma);
        if (d == 17) target += normal_lpdf(performance17[i, r] | mu, sigma);
        if (d == 18) target += normal_lpdf(performance18[i, r] | mu, sigma);
      }
    }
  }
}

レースの頭数ごとにパフォーマンスを順序付き変数として扱っている点に注意されたい．なお，入力データのHorseIDおよびJockeyIDは各行が1つのレースと対応した行列であり，そのレースで走った馬と騎乗した騎手が整数値のIDとして格納されている．

「非現実的な」モデル？

このモデルは暗黙のうちにさまざまな仮定をおいている．そのうちのいくつかを列挙してみよう．

  • 馬と騎手の能力が独立であること（＝騎手と馬の「相性」は考慮しない）
  • 馬や騎手の能力は時間的に変化しないこと
  • その他のあらゆるレースの条件（芝/ダートや距離，コース等）は考慮しないこと

モデルフィッティング

まず能力パラメータの事後分布をみてみよう．馬の能力（\(\mu_{h}\)）の推定値（事後中央値）の上位10頭は以下のようになった．

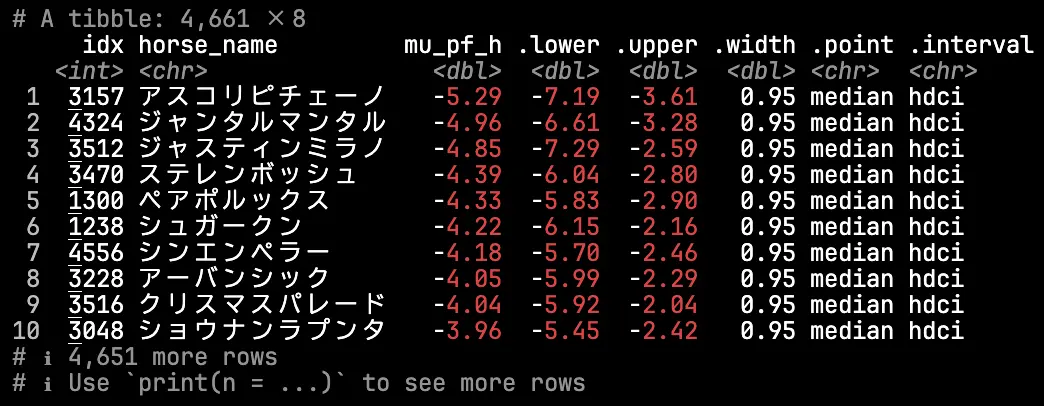
2024年のダービー前の勢力図をおぼろげに思い出すと，まずまず妥当な評価をしているのではなかろうか．

「能力」の解釈

このモデルではコース適性などを考慮せず対戦成績のみに応じて能力を数値化しているので，この結果がなんらかの序列を意味すると言われると違和感を覚える人も多いかもしれない．

モデルでは「馬の能力」と「騎手の巧みさ」を一つの次元で扱っているため，必然的に「成績があまり良くない鞍上で好成績を残す馬」ほど馬自体の評価は高くなる．アスコリピチェーノはルメール騎手を鞍上に迎えたNHKマイルでジャンタルマンタルの2着に敗れたものの最上位評価となっているが，以前に北村宏騎手と3戦して2勝を挙げているのが効いているのかもしれない．松若騎手とのコンビで期間内5戦2勝2着2回のペアポルックスが評価が高いのもおそらく同様の理由であろう．

翻って，騎手の能力\(\mu_{j}\)についてはどうだろうか．

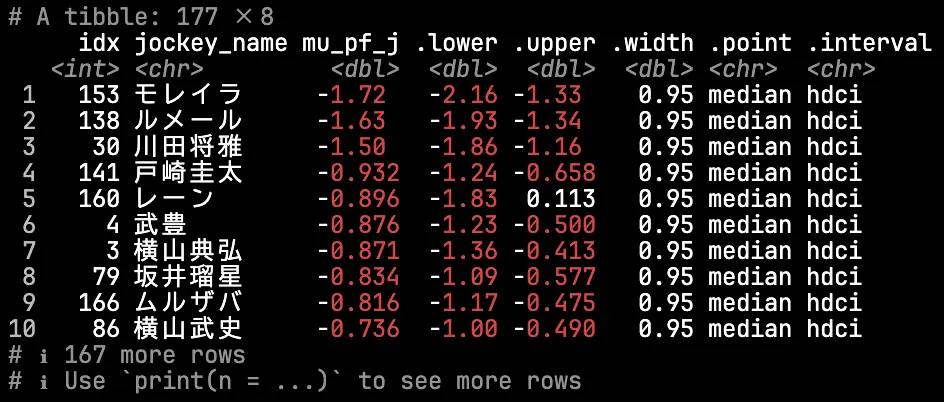
リーディング上位の騎手がちゃんとランクインしており，おおむね直感に沿った結果といえそうだ．ルメール・川田・モレイラの3強は流石の貫禄である．

「騎手3割・馬7割」？

馬の能力と騎手の巧みさの分布のパラメータ（\(\sigma_{\mu_h},\sigma_{\mu_j}\)）の推定結果を用いると，「馬と騎手のどちらがどのくらいパフォーマンスを規定するのか」という問いに対して定量的に答えを与えることができる．

実際に分散比を計算すると，馬の能力の分散は騎手のおよそ10倍だった（\(\sigma_{\mu_h}^2 / \sigma_{\mu_j}^2\) = 10.26，95％CI[7.23, 14.10]）．競馬ファンなら「騎手3割・馬7割」という格言を耳にしたことがあると思うが，この結果を素直に解釈すれば正しくは「騎手9分・馬9割1分」といった格好である．

もっとも今回の場合，実力差が大きい若駒のレースにデータが限定されている点に注意が必要だろう．古馬のレースまで含めると相対的に馬の能力の分散が小さくなり，格言どおりの「騎手3割・馬7割」に近づく可能性は十分にありそうだ．

やっぱり予測がしたい！

モデルフィッティングするだけでも十分に楽しいが，やはり気になるのはこの結果が結果の予測に使えるかどうかである．便利なことに，本モデルの枠組みでは馬と騎手の任意の組み合わせについてレース結果の予測分布を得ることができる．以下では，フィッティングの際に除外していたダービーを対象に（参考：netkeiba），事後分布に基づくサンプル外予測を実施してみよう．

予測分布の生成

Stanのgenerated_quantitiesブロックに記述を追加することで，ターゲットとなるレースでのパフォーマンスの予測分布を得ることができる．また，パフォーマンスが最も良かった馬を記録することでモンテカルロシミュレーションを行うことも可能だ．

data {
  // ...
  int N_race_target;
  array[N_race_target] int HorseID_target;
  array[N_race_target] int JockeyID_target;
}

// ...

generated quantities {
  array[N_race_target] real target_performance;
  array[N_race_target] real win = rep_array(0.0, N_race_target);
  
  // Predictive performance
  for (i in 1:N_race_target) {
    real mu = mu_pf_h[HorseID_target[i]] + mu_pf_j[JockeyID_target[i]];
    real sigma = sqrt(square(sigma_pf_h[HorseID_target[i]]) + square(sigma_pf_j[JockeyID_target[i]]));
    target_performance[i] = normal_rng(mu, sigma);
  }

  // Determine winner
  for (i in 1:N_race_target) {
    if (target_performance[i] == min(target_performance)) {
      win[i] = 1.0;
    }
  }
}

シミュレーションにより得られる出走各馬の勝率の点推定値をまとめると，以下のようになった．

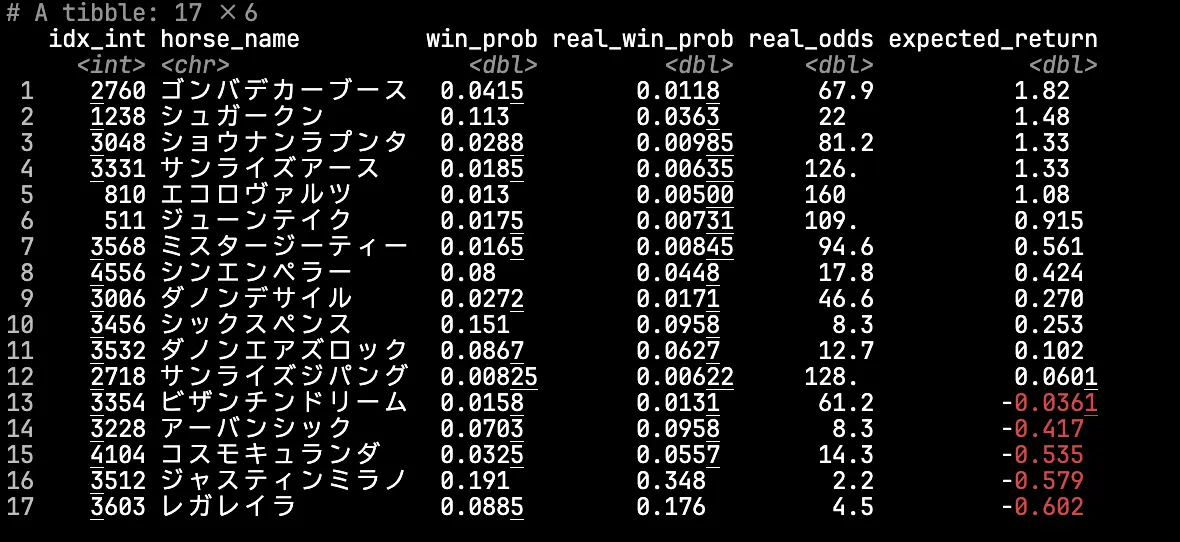
実際のオッズ（real_odds）や市場の主観的な勝率（real_win_prob）と比べるとモデル上の推定値（win_prob）の分散は小さくなっているが，大きくは外していないように思われる．

なお期待リターンが最も高かったのはゴンバデカーブースであった．NHKマイルでは世代最強格のジャンタルマンタルとアスコリピチェーノが連を占めるなかで4着に入っており，モデルが距離適性などの要素を無視していることを踏まえると合点がいく．

他の指標との比較

参考までに，JRA-VANが提供しているマイニング指数およびTARGET frontier JVで利用可能なZI指数（該当馬の前走について，さまざまな観点からパフォーマンスを指数化したもの）との比較を示しておく．

着順 馬名 オッズ 推定勝率順位 DM指数順位 ZI指数順位
1 ダノンデサイル 46.6 11 10 11
2 ジャスティンミラノ 2.2 1 2 1
3 シンエンペラー 17.8 6 5 6
4 サンライズアース 125.9 12 13 14
5 レガレイラ 4.5 4 12 10
6 コスモキュランダ 14.3 9 14 4
7 シュガークン 22.0 3 8 3
8 エコロヴァルツ 160.0 16 17 13
9 シックスペンス 8.3 2 7 1
10 ジューンテイク 109.4 13 3 8
11 アーバンシック 8.3 7 15 7
12 サンライズジパング 128.5 17 11 16
13 ゴンバデカーブース 67.9 8 6 9
14 ダノンエアズロック 12.7 5 9 12
15 ショウナンラプンタ 81.2 10 1 5
16 ミスタージーティー 94.6 14 4 17
17 ビザンチンドリーム 61.2 15 16 14

着順との順位相関を計算すると，推定勝率が\(\rho=0.385\)，DM指数が\(\rho=-0.037\)，ZI指数が\(\rho=0.375\)といった具合である．このレースの予測だけから精度について云々するのは難しいが，使用しているデータの割には悪くない精度が出るものである．

ポートフォリオ最適化

各馬の勝率とオッズを所与とすれば，その後の戦略は金融工学の領域である．以下ではclassicなポートフォリオ最適化手法であるKelly基準 (Kelly, 1956) を用いて，「長期的に資産を最大化するために幾らを投資すればよいか」を具体的に計算してみよう．

以下はKelly基準に基づいて最適な投資配分を計算するRコードである．最適配分の探索は制約付きの非線形計画問題となるため，ここでは差分進化アルゴリズムにより最適化をおこなう．なお，実装にあたっては Smoczynski & Tomkins (2010) を参考にした．

library(DEoptim)

calculate_kelly_allocation <- function(probabilities, returns, total_capital) {
  N <- length(probabilities)

  objective_function <- function(f) {
    f_total <- sum(f)
    if (f_total > 1 + 1e-6) {
      penalty_sum <- 1e10 * (f_total - 1)^2
      return(1e10 + penalty_sum)
    }
    log_terms <- numeric(N)
    for (i in 1:N) {
      growth_factor <- 1 + (1 + returns[i]) * f[i] - f_total
      if (growth_factor <= 1e-6) {
          penalty_log <- 1e30 * (1e-6 - growth_factor)^2
          return(1e30 + penalty_log)
      }
      log_terms[i] <- probabilities[i] * log(growth_factor)
    }
    return(-sum(log_terms))
  }

  # Differential Evolution Optimization
  opt_result <- DEoptim(
    fn = objective_function,
    lower = rep(0, N),
    upper = rep(1, N),
    control = DEoptim.control(
        NP = 15 * N,
        itermax = 1000,
        parallelType = 1,
        trace = FALSE
    )
  )

  f_star <- pmax(0, opt_result$optim$bestmem)
  f_star[f_star < 1e-4] <- 0
  bet_amounts <- f_star * total_capital
  max_log_growth_rate <- -opt_result$optim$bestval
  
  return(list(
    f_star = f_star,
    bet_amounts = round(bet_amounts),
    max_log_growth_rate = max_log_growth_rate
  ))
}

各馬の勝率の点推定値と実際のオッズをもとに，最適な投資配分を求めよう．

prob_table <- readRDS("prob_table.rds") # 整形済みデータ

# Input
probabilities <- prob_table$win_prob  # 勝率の推定値
returns <- prob_table$real_odds - 1   # 的中時のリターン
total_capital <- 100 # 10000 yen

# Estimation
set.seed(777)
res <- calculate_kelly_allocation(
  probabilities = probabilities,
  returns = returns,
  total_capital = total_capital
)

# Allocation
sum(res$bet_amounts)
prob_table %>%
  transmute(
      idx_int, horse_name,
      real_odds,
      bet_amount = res$bet_amounts
  )

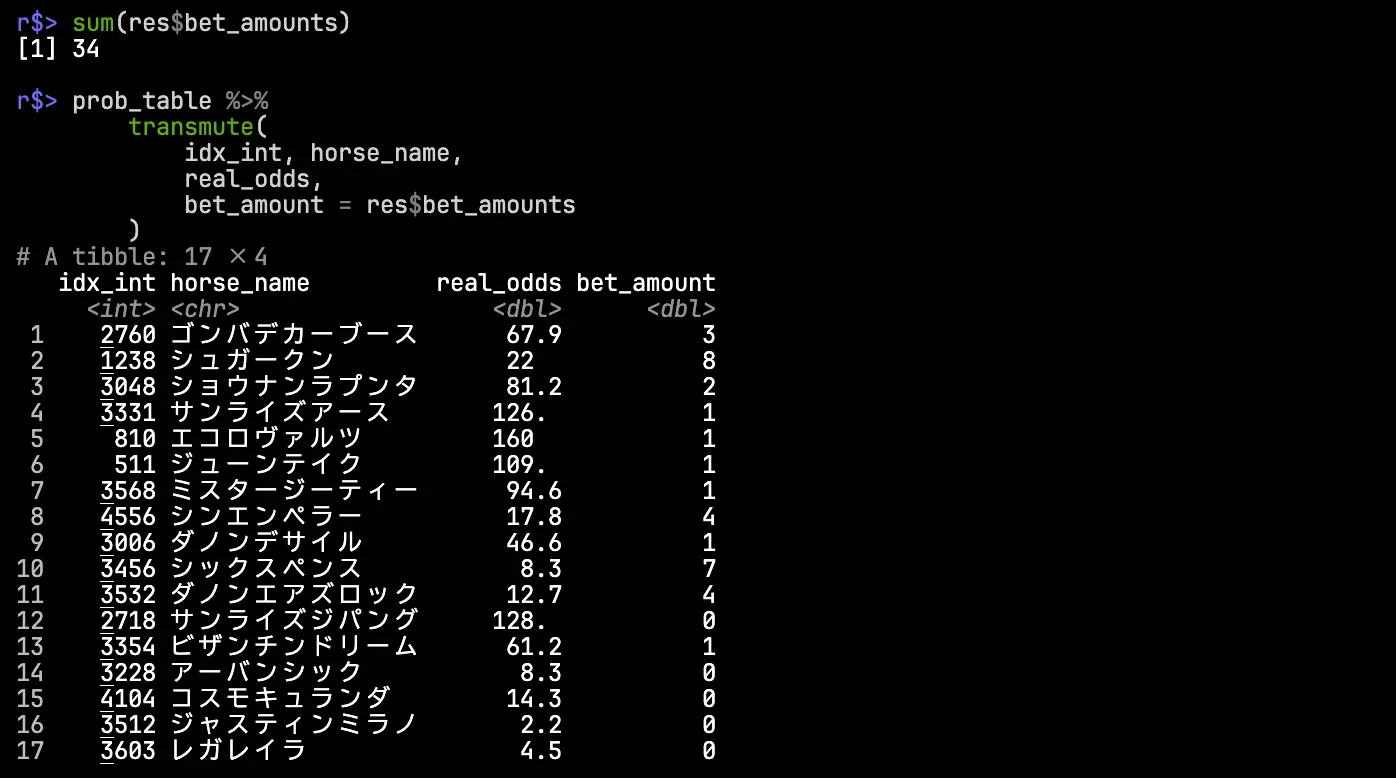
結果，資産が10000円の状況における最適な投資額は3400円となり，単勝12点買いが最適と判断された（期待リターンが負になるはずのビザンチンドリームがなぜか買い目に入っているが，これは数値計算上の誤差によるものと思われる．対策としては，あらかじめ期待リターンが負になる馬を除外するなどの変更や初期解の調整などがありうる）．

結果，見事にダノンデサイルの単勝46.6倍を引っ掛け（100円），当該レースの収支は+1260円となった．やったね．

「プラス収支」の難しさ

ポートフォリオの最適性は，兎にも角にも勝率の推定が正確であることによって理論的に保証される．現状の推定は明らかに穴サイドを過大に評価しているため，残念ながら実用には程遠いと言わざるを得ない（今回に限れば典ちゃんのおかげで高目を引けたわけだが）．

通常のパリミュチュエル市場ではテラ銭が控除された残りが勝者に配分されるため，市場が完全に効率的であればいかなる買い目でも期待リターンが正になることはなく，Kelly基準による配分比率は0となる．要するに，何らかのかたちでオッズが歪んでいないと儲けは期待できないということだ．ちなみに，競馬をはじめとする多くのパリミュチュエル市場では人気薄が過大評価されるバイアス（アノマリー）の存在が経験的に知られており (Snowberg & Wolfers, 2010)，特に三連単などの点数が多い馬券でその影響は顕著に見られる．

勝率の推定精度のみならず，実際の馬券購入時には締め切り前のオッズの変動といった種々の不確実性を考慮にいれる必要がある．そのため，理論的な最適値よりもリスク回避的な戦略を取る（投資額を割り引くなど）のが基本的な立ち回りになるだろう．

まとめ

本稿のモデルはごく限られたデータに基づくものであり，予測精度の点で実用からは遠くかけ離れている．一方，巷に跋扈する「予想理論」の多くが論者の直観や曖昧な自然言語に基づいているため，しばしば後知恵や恣意的な解釈に汚染されている（したがって，当人が主張する「理論」そのものが外部から検証不可能である）ことを踏まえると，素朴だが明確に定義されたトイモデルによるアプローチにもいささかの存在意義はあるだろう．この点は科学哲学における議論と深く関連しているので，興味のある方は Weisberg (2012) などを参照されたい．

今年も禄に現地観戦できていないので，なんとか秋の府中開催が終わる前に現地まで足を運びたいものである．どうにか秋天とか行けないかなあ．てかベラジオオペラは出ないのね．

References

Kelly, J. (1956). A new interpretation of information rate. IEEE Transactions on Information Theory, 2(3), 185–189.
Smoczynski, P., & Tomkins, D. (2010). An explicit solution to the problem of optimizing the allocations of a bettor’s wealth when wagering on horse races. The Mathematical Scientist, 35, 10–17.
Snowberg, E., & Wolfers, J. (2010). Explaining the Favorite–Long shot bias: Is it risk-love or misperceptions? The Journal of Political Economy, 118(4), 723–746.
Weisberg, M. (2012). Simulation and similarity: Using models to understand the world. Oxford University Press.